Vonk & Stapel
Het is treurig gesteld met de kwaliteit en integriteit in de Sociale Psychologie.
Op 25 augustus 2011 verscheen in de RSS-feed van diverse kranten: “Vleeseters zijn egoïstischer en asocialer”: een bericht van de Radboud Universiteit naar aanleiding van een onderzoek van Stapel, Zeelenberg en Vonk. Ik geloofde er niets van.
Ik zag Roos Vonk twitteren (tot mijn stomme verbazing), dat zij via de Radboud Universiteit dit persbericht had laten uitgaan, maar dat het onderzoek nog niet gepubliceerd was. Sterker nog: er was zelfs nog geen artikel geschreven, er was alleen maar een samenvatting voor de pers. In mijn ogen een volstrekt onethisch gedrag voor een hoogleraar.
Ik vroeg de auteurs of ik alle informatie kon inzien. Roos Vonk antwoordde dat ze mij zowel de “samenvatting voor de pers” als de originele meetresultaten zou sturen. Het eerste kreeg ik snel, maar de rest heb ik (uiteraard) nooit ontvangen (want later bleek die helemaal niet te bestaan).
Vonk: arrogant en bevooroordeeld
Roos Vonk liet zich in haar mails naar mij meteen van haar meest arrogante kant zien. Ik moest wel objectief blijven, schreef ze [4]. Maar door het naar buiten brengen van de resultaten van een nog niet eens geschreven onderzoek laat ze nu juist zien dat ze zelf niet weet wat objectiviteit is. Dat ze daar echt niets van snapt, bleek nog eens in een interview dat ik 30 augustus in het Leidsch Dagblad aantrof. Het is te onthullend om er niet uit te citeren.
RV: … maar ik denk dat rundvlees egoïstischer maakt.
LD: Waarom?
RV: Rood vlees geeft meer status. Het is meer een mannending. Een koe is
tenslotte moeilijker te vangen dan een varken.
LD: Maar een varken kan toch harder rennen dan een koe?
RV: Oh, is dat zo? Dat wist ik niet. Maar als je wilt weten waarom mannen van rood
vlees houden kun je dat misschien beter aan die vleesetende vrachtwagenchauffeurs
vragen.
Nadat ik dit gelezen had besloot ik zeker over dit “onderzoek” te gaan publiceren. Want wat hier staat is natuurlijk ook nog eens enorme onzin: Roos Vonk heeft kennelijk een hekel aan rood-vlees-etende mannen en ze denkt daarom dat rood-vlees-eten egoïstischer maakt.
De bevooroordeeldheid maakt Vonk ongeschikt voor onderzoeken die haar passies (dierenwelzijn) raken. Als ze een te-mooi-om-waar-te-zijn-resultaat te zien krijgt, stelt zij zichzelf niet de voor de hand liggende vraag hoe dat dan kan, en al helemaal niet de vervolgvragen – als dit zo evident is, waarom hebben we dat eerder gemist en wat kunnen we nog meer met onze methodes doen. Nee, ze kraait triomfantelijk: “Zie je wel, ik had gelijk!”
Belabberde methodes en slechte statistiek
Ik wist weinig tot niets van de gewoontes in de sociale psychologie, ik was bijvoorbeeld verrast dat hun steekproeven helemaal niet zo a-select zijn. Ze pakken gewoon een schoolklas met 32 pubers of een groep van hun eigen studentes. Wist ik veel, ik vond N=32 alleen maar heel mager, maar nu blijkt dat een volle schoolklas te zijn.
Het eerste dat mij meteen opviel in de samenvatting [1] was dat die slordig was. De resultaten van 2(a) en 2(b) zijn verwisseld. Het tweede dat direct opviel is dat de proefopzet zo verschrikkelijk klungelig was. Is dat de “state of the art” in de sociale psychologie? Maar goed, de cijfers, daar ging het mij in eerste instantie om. Ik dook in het eerste experiment.
Zonder de origineel metingen is het lastig een gevoel te ontwikkelen bij deze cijfers. Bij het eerste experiment (zie figuur 1) worden twee groepen vergeleken op een drietal kenmerken die alle drie significant verschillen. Kijken we naar de eerste regel: een standaardeviatie (σ) van 1.6 – voor een score op een schaal van 1-7 en gemiddelde (μ) van 5,1: is dat veel of weinig? In ieder geval is verdeling scheef, want het 95%’s-gebied loopt bij benadering van μ-2σ naar μ+2σ, maar dat valt dus deels buiten de schaal.
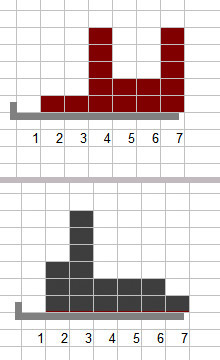 Ik kreeg er geen goed gevoel bij – ik schreef daarom even een random generator in Python die een paar verdelingen 5.1 en 3.8(1.6) produceert. Zoals ik het begreep werd de groep van 32 in twee groepen van (ongeveer) 16 gesplitst, en moest ik dus met 16 trials dit resultaat bereiken. Makkelijk zat: zie het plaatje rechts. De trials komen ook nog uit een klokvormige verdeling met een gemiddelde van 4. Maar de steekproef is zo klein dat het steekproef gemiddelde alle kanten uit kan gaan.
Ik kreeg er geen goed gevoel bij – ik schreef daarom even een random generator in Python die een paar verdelingen 5.1 en 3.8(1.6) produceert. Zoals ik het begreep werd de groep van 32 in twee groepen van (ongeveer) 16 gesplitst, en moest ik dus met 16 trials dit resultaat bereiken. Makkelijk zat: zie het plaatje rechts. De trials komen ook nog uit een klokvormige verdeling met een gemiddelde van 4. Maar de steekproef is zo klein dat het steekproef gemiddelde alle kanten uit kan gaan.
Boven het gemiddelde 5.1, onder 3.8. Beide met een σ= 1.6. Dan krijg je een beetje een gevoel wat dit eigenlijk betekent: als je in het bovenste diagram drie bangerikken die een 7 scoren vervangt door drie 3-en is er al een evenwichtige verdeling. Maar om dit nou significant te vinden? Dus als het toeval drie erg beïnvloedbare personen in de eerste groep plaatst (kans 1/8 !), wordt het dan al significant? Natuurlijk niet.
Kennelijk rammelde de gebruikte statistiek dus aan alle kanten. Misschien de verkeerde toets gebruikt? Of had ik het fout en was N toch niet 32? Werd soms bedoeld dat de twee groepen 32 groot zijn? Impulsief stuur ik een mailtje. De volgende dag mailt Stapel mij terug via zijn mobiel [6], kort, nee het is echt 32 voor het totaal.
Onmogelijke gegevens
Tot aan het mailtje zag ik alleen maar foute statistiek. Dan begint het me ook op te vallen hoe onmogelijk sommige cijfers zijn. In de derde regel van hetzelfde experiment staan cijfers die niet eens mogelijk zijn. 44% en 15% zijn samen tegelijk onmogelijk bij N=32. Okay, dan zal ik moeten publiceren dat de getallen niet kunnen kloppen. Het is mathematisch onmogelijk. Ook de 60% en 20% bij het volgende experiment zijn onmogelijk.
Dat is simpel zodra je het ziet. Ingewikkelder wordt het als ik constateer dat er onmogelijke standaarddeviaties in staan. Ik heb dat uit mijn concept rapport weggelaten – maar het is toch wel illustratief.
Figuur 3.
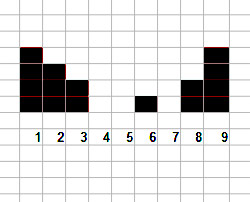 Hier heb ik twee stukjes uit de resultaten van het tweede experiment geknipt. Op een schaal van 1-9 vinden we 5 keer een standaarddeviatie van ruim 3. Dat is nog groter dan de σ van een uniforme verdeling. Bij een uniforme verdeling is het histogram voor elk hokje (ongeveer) even groot. Hier hebben we dus een verdeling nodig waar meer metingen in de uiteinden dan bij het gemiddelde zitten. Het plaatje rechts geeft het histogram van een 4.6 (3,5) verdeling. Mijn randomgenerator vond zelfs na een miljoen pogingen geen 4.6(3.6) verdeling.
Hier heb ik twee stukjes uit de resultaten van het tweede experiment geknipt. Op een schaal van 1-9 vinden we 5 keer een standaarddeviatie van ruim 3. Dat is nog groter dan de σ van een uniforme verdeling. Bij een uniforme verdeling is het histogram voor elk hokje (ongeveer) even groot. Hier hebben we dus een verdeling nodig waar meer metingen in de uiteinden dan bij het gemiddelde zitten. Het plaatje rechts geeft het histogram van een 4.6 (3,5) verdeling. Mijn randomgenerator vond zelfs na een miljoen pogingen geen 4.6(3.6) verdeling.
Aan het plaatje kun je ook zien dat 1.9(3,2) helemaal niet kan bestaan, want dan heb je negatieve getallen nodig. Mooier dan dit kan ik niet laten zien dat de dame en heren geen enkel gevoel hebben voor getallen. Ik haalde het helaas weg uit het concept.
Op 2 september stuurde ik een concept rapport [2] naar de drie co-auteurs: Vonk, Stapel en Zeelenberg. Ik krijg geen reactie. Ik herschrijf het enigszins voor een breder publiek, laat de meest technische stukken weg en zet het op 6 september op foodlog.nl [3]. De volgende dag, om een uur of drie, komt het bericht over Stapel’s fraude naar buiten.
Fraude zonder onderzoeksprotocol is kinderlijk eenvoudig
Aan fraude had ik echt nooit gedacht, ik was alleen enorm verbijsterd door de grote hoeveelheid slordigheden. Maar achteraf weten we nu wel heel zeker dat dit óók een van de door Stapel van A tot Z uit de duim gezogen onderzoeken is.
Mijn Python generator laat zien dat fraude kinderlijk eenvoudig is als er geen onderzoeksprotocol is. Stapel is stom geweest, hij heeft in dit geval alleen maar de resultaten verzonnen, en niet de meetgegevens. Daardoor staan er getallen bij die niet mogelijk zijn. Maar als je iets meer verstand van programmeren hebt, dan schrijf je gewoon een generator die net zo lang door gaat tot hij een steekproef heeft gegenereerd die de gewenste waarden geeft. De meeste waarden kwamen binnen een milliseconde er uit rollen. Wil je ook correlaties hebben tussen de getallen verticaal: geen probleem, staat-ie gewoon wat langer te stampen.
Wat je ook ziet in de bovenste twee diagrammen is dat je maar een paar scores hoeft te veranderen om een vrij radicaal ander beeld te krijgen. Dus ook als er wel echt een onderzoek is geweest, er hoeven maar een paar scores verkeerd opgeschreven te worden en — bingo! Het kan zelfs een vergissing zijn. Alleen daarom is een onderzoeksprotocol essentieel.
Vonk ontsnapt dank zij Stapel
We weten hoe het verder afloopt. Stapel wordt uiteraard de laan uitgestuurd, Roos Vonk’s handelen zou worden getoetst door de ethische commissie van de Radboud. Maar na een paar maanden komt Roos Vonk er af met een berisping. In het korte persbericht hierover overheerst de constatering dat Vonk geen fraude heeft gepleegd (ja, dat was mij bekend), en staat er over het onderzoek zelf alleen heel voorzichtig dat de gebruikte opzet ondermaats was. Niet helemaal helder is wat zij er mee precies bedoelden.
Mijn kritiek staat echter nog steeds 100% overeind. En met mij zijn er veel meer publicisten van mening dat ze wel erg makkelijk hier mee weg komt. De methode deugde al niet, de statistiek deugde niet, de conclusies mochten niet zo getrokken worden, en er had al helemaal geen persbericht uit mogen gaan voordat het artikel geschreven, beoordeeld en gepubliceerd was. De kritiek op de methode en de statistiek slaat op alle drie de co-auteurs, maar de rest alleen op Vonk, want inmiddels is duidelijk geworden dat de genoemde conclusies en persberichten een solitaire actie van haar waren.
Op Foodlog schreef ik kortgeleden daarom nog een naschrift toen het oordeel van de ethische commissie naar buiten kwam:
Aangekondigd was dat het oordeel van de ethische commissie eind september zou verschijnen. Het is bijna twee maanden later. Het rapport van de commissie is niet openbaar. Maar uit de enorme vertraging blijkt al dat dit oordeel niet op een gemakkelijke manier tot stand is gekomen. Het zou mij niets verbazen als er veel advocaten aan te pas zijn gekomen en als er over elke punt en komma is onderhandeld.
Het is een geen-vlees-en-geen-vis oordeel (“no pun intended”) waar het onethisch handelen wordt verstopt achter de data-fraude. Maar de kern wordt slechts terloops genoemd, en dat is dat de opzet van het onderzoek al onvoldoende wetenschappelijk was. Wat door Vonk niet is en niet wordt onderkend en erkend. Die fraude kwam later. Stapel, Zeelenberg en Vonk hebben al broddelwerk afgeleverd bij het verzinnen van dit onderzoek. De vraagstelling deugde niet, de proefopzet deugde niet, en andere mogelijke verklaringen van te vinden verschillen werden a priori uitgesloten. Het was en is een bevooroordeelde vraagstelling.
Vonk weet het verschil niet te maken tussen haar “wetenschappelijk” werk en haar activisme. Dit is dus een hoogleraar die een “opmerkelijk” onderzoek voortijdig in een persbericht zet, en dan met activistische praat uitlegt waarom het resultaat echt niet zo vreemd is. De enkele kritische toeschouwers en journalisten die lieten zien dat haar observatie niet klopten, werden weggesnauwd.
Inmiddels twittert Roos Vonk weer vrolijk verder over dierenleed en natuurbehoud. Ik ben het dan vaak nog met haar eens ook. Maar Roos, kom eens echt uit je hok en ga deze discussie met mij aan.
Noten…
- De “samenvatting voor de pers” (pdf) van 25 augustus 2011
- Mijn concept naar Vonk, Stapel en Zeelenberg (pdf) van 2 september 2011
- Publicatie op foodlog.nl (origineel, pdf) en hier.
- Mail van Vonk [1]
- Mail van Vonk [2]
- Mail van Stapel (N=32)

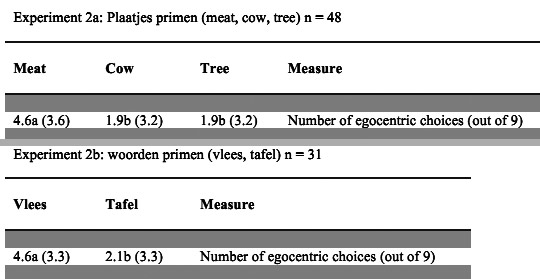
“De volgende dag mailt Stapel mij terug via zijn mobiel [6], kort, nee het is echt 32 voor het totaal.”
In [6] lees ik echter jouw vraag als: “betekent het nu zus of betekent het nu zo?” Waarop het antwoord is: “Ja dat betekent het.” Daar kun je m.i. zowel zus als zo uit concluderen (ofwel N= 32 of N=2×32).
Of heb ik nou iets niet goed begrepen? Heb ook nooit op de Kath. Univ. Tilburg gezeten.
Ja Albert, dat was ook mijn eerste gedachte. Op de vraag is het een jongen of een meisje komt het logisch correcte antwoord “Ja”. Maar toen zag ik een haastig naar college lopende professor voor me, die even snel een maar half gelezen mailtje op zijn iPhone beantwoordt, dus dat het op de eerste helft slaat. Bovendien – alleen wiskundigen maken dit soort grappen, want gewone mensen vinden het niet leuk.
Stapel is geen wiskundige, dus kun je hem niet op gelijk niveau behandelen (om wel meer redenen niet trouwens). Maar ik zou uit zo’n flodderig antwoord geen keiharde conclusie durven trekken. Zeker als jouw verhaal wel opgaat bij 32 en neit bij 2 x 32 (maar ik weet niet of dàt zo is).
@Albert, “stapel is geen wiskundige”. Voor wetenschappers aan een universiteit zou dit gesneden koek moeten zijn. Het gros is zelfs wiskunde A van het VWO. Neen, Stapel fraudeert, maar Vonk laat zien niets van onderzoeksmethodes, statistiek en goede wetenschap te weten.