Een jaar heeft twaalf maanden, een klok twaalf uren: wat als we een tijdreeks als de bewegingen van een wijzer van de klok afbeelden? Het zal wel geen nieuw idee zijn, maar het helpt wel de invloeden van seizoenen inzichtelijk te maken. Andere aspecten worden natuurlijk lastiger te zien.
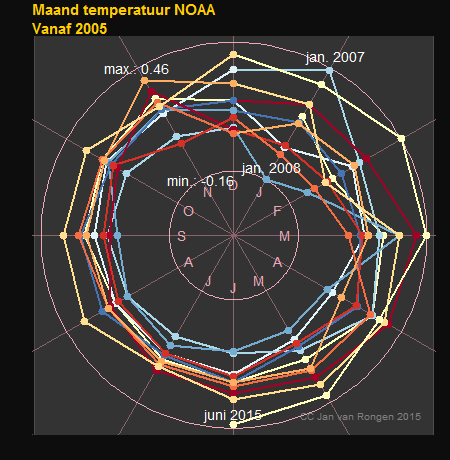
Met januari op 1 uur en doortellend naar december op 12 uur zetten we de globale temperaturen uit vanaf 2005 volgens de berekeningen van NOAA. Wat mij opvalt is dat je de grilligheid van de veranderingen vooral voorkomen als het zomer is op het Zuidelijke Halfrond. Als het hier zomer is zijn de verschillen veel beperkter. We zien dus wellicht in dit plaatje de gevolgen terug van de grotere bewegingen van oceaanstromingen op het zuidelijke halfrond. De natuurlijke variabiliteit van de globale temperatuur lijkt groter te zijn in de periode Nov-Maart dan in de periode Maart-Nov.
Verder zien we uiteraard dat op dit ogenblik de temperatuur op weg is naar een nieuw record. De juni temperatuur is zeer ongewoon hoog (voor een juni).
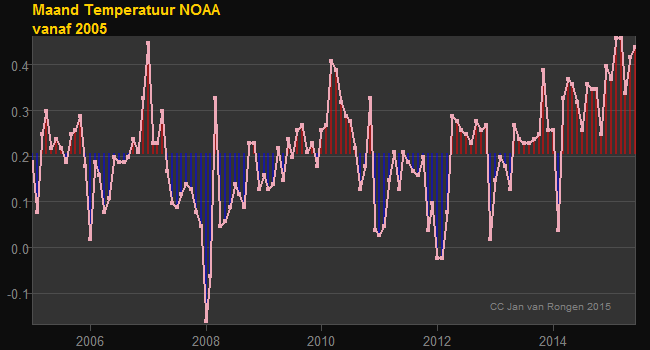
Allemaal zaken die we niet zomaar in de “gewone” plot zien over dezelfde periode:
We zien hier eigenlijk alleen drie heftige sprongen(2007, 2008 en iets mindert 2010) maar weinig anders.
Terug naar de gedachte dat de variaties groter zijn in onze wintermaanden. Wellicht wordt dat duidelijker als we van alle jaren de maanden plotten waar het maximum of het minimum van de temperatuur in dat jaar werd berekend. Dat heb ik gedaan voor de hele periode van de NOAA-data – en het resultaat is opmerkelijk en duidelijk, zowel de maxima (rood, dicht bij de buitenste ring) als de minima (blauw, dicht bij de binnenste ring) vallen vaker in de maanden oktober tot en met maart dan in de andere maanden.
NB de puntjes zijn een beetje naast de lijn gezet, dan vloeien ze iets minder in elkaar over.
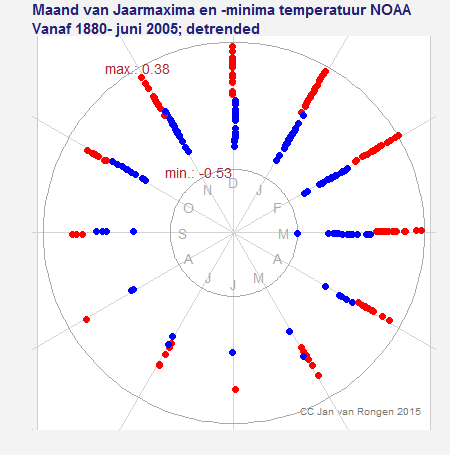Ook hier moet ik nog even een slag om de arm houden, want voor de variabiliteit moet je naar de gegevens kijken minus een lange-termijn trend, bijv. minus de “smooth”van een langjarig gemiddelde. Dat is bijna net zo snel gemaakt als bedacht, we scheiden daardoor nu ook netjes de blauwe en rode puntjes in het volgende diagram. Duidelijker kan het eigenlijk niet: veel minder variabiliteit in de zomers van het Noordelijke Halfrond.
Techniek
Het makkelijkst maak je deze diagrammen in R met complexe getallen De temperatuur is dan de amplitude; deze wordt voor de maand $$m$$ vermenigvuldigd met $$e^{{-(m+2).i. \pi}/6}$$